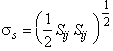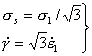CHAPTER 1

DEFORMATION MECHANISMS AND DEFORMATION-MECHANISM MAPS

1.1 Atomic Processes and Deformation Mechanisms

1.2 Rate-Equations

1.3 Deformation-Mechanism Maps

1.4 A Warning

References for Chapter 1

CRYSTALLINE Solids deform plastically by a number of alternative, often competing, mechanisms. This book describes the mechanisms, and the construction of maps which show the field of stress, temperature and strain-rate over which each is dominant. It contains maps for more than 40 pure metals, alloys and ceramics. They are constructed from experimental data, fitted to model-based rate-equations which describe the mechanisms. Throughout, we have assumed that fracture is suppressed, if necessary, by applying a sufficiently large hydrostatic confining pressure.

            The first part of the book (Chapters 1-3) describes deformation mechanisms and the construction of deformation-mechanism maps. The second part (Chapters 4-16) presents, with extensive documen­tation, maps for pure metals, ferrous and non­ferrous alloys, covalent elements, alkali halides, carbides, and a large number of oxides. The final section (Chapters 17-19) describes further develop­ments (including transient behavior, the influence of pressure, behavior at very low and very high strain rates) and the problem of scaling laws; and it illustrates the use of the maps by a number of simple case studies.

            The catalogue of maps given here is, inevitably, incomplete. But the division of materials into iso-mechanical groups (Chapter 18) helps to give in­formation about materials not analyzed here. And the method of constructing maps (Chapter 3) is now a well-established one which the reader may wish to apply to new materials for himself

            Plastic flow is a kinetic process. Although it is often convenient to think of a polycrystalline solid as having a well defined yield strength, below which it does not flow and above which flow is rapid, this is true only at absolute zero. In general, the strength of the solid depends on both strain and strain-rate, and on temperature. It is determined by the kinetics of the processes occurring on the atomic scale: the glide-motion of dislocation lines; their coupled glide and climb; the diffusive flow of individual atoms; the relative displacement of grains by grain boundary sliding (involving diffusion and defect-motion in the boundaries); mechanical twinning (by the motion of twinning dislocations) and so forth. These are the underlying atomistic processes which cause flow. But it is more convenient to describe polycrystal plasticity in terms of the mechanisms to which the atomistic processes contribute. We therefore consider the following deformation mechanisms, divided into five groups.

The mechanisms may superimpose in complicated ways. Certain other mechanisms (such as super­plastic flow) appear to be examples of such com­binations.

            Plastic flow of fully-dense solids is caused by the shearing, or deviatoric part of the stress field, σ_s. In terms of the principal stresses σ₁, σ₂ and σ₃:

or in terms of the stress tensor σ_ij:

(Very large hydrostatic pressures influence plastic flow by changing the material properties in the way described in Chapter 17, Section 17.4, but the flow is still driven by the shear stress σ_s.)

            This shear stress exerts forces on the defects—the dislocations, vacancies, etc.—in the solid, causing them to move. The defects are the carriers  of deformation, much as an electron or an ion is a carrier of charge. Just as the electric current depends on the density and velocity of the charge carriers, the shear strain-rate,  , reflects the density and velocity of deformation carriers. In terms of the principal strain-rates , and , this shear strain-rate is:

or, in terms of the strain-rate tensor :

For simple tension, σ_s and  are related to the tensile stress σ₁ and strain-rate   by: 

            The macroscopic variables of plastic deformation are the stress σ_s, temperature T, strain-rate  and the strain γ  or time t.  If stress and temperature are prescribed (the independent variables), then the con­sequent strain-rate and strain, typically, have the forms shown in Fig. l.la. At low temperatures ( ~ 0.1 T_M  , where T_M is the melting point) the material work-hardens until the flow strength just equals the applied stress. In doing so, its structure changes: the dislocation density (a microscopic, or state variable)   increases, obstructing further dislocation motion and the strain-rate falls to zero, and the strain tends asymptotically to a fixed value. If, instead, T  and  are prescribed (Fig. 1.1b), the stress rises as the dislocation density rises. But for a given set of values of this and the other state variables S_i (dislocation density and arrangement, cell size, grain size, precipitate size and spacing, and so forth) the strength is determined by T and , or (alternatively), the strain-rate is determined by σ_s and T.

            At higher temperatures (~ 0.5T_M) , polycrystalline solids creep (Fig. 1.1, centre). After a transient during which the state variables change, a steady state may be reached in which the solid continues to deform with no further significant change in S_i. Their values depend on the stress, temperature and strain-rate, and a relationship then exists between these three macroscopic variables.

Fig. 1.1. The way in which σ_s ,T,  and γ are related for materials (a) when σ_s and T are prescribed and (b) when  and T are prescribed, for low temperatures (top), high temperatures (middle) and very high temperatures (bottom).

            At very high temperatures (~ 0.9T_M) the state variables, instead of tending to steady values, may oscillate (because of dynamic recrystallization, for instance: Fig. 1.1, bottom). Often, they oscillate about more or less steady values; then it is possible to define a quasi-steady state, and once more, stress, temperature and strain-rate are (approximately) related.

            Obviously, either stress or strain-rate can be treated as the independent variable. In many engineering applications—pressure vessels, for in­stance—loads (and thus stresses) are prescribed; in others—metal-working operations, for example—it is the strain-rate which is given. To simplify the following discussion, we shall choose the strain-rate   as the independent variable. Then each mechan­ism of deformation can be described by a rate equation  which relates  to the stress σ_s, the temperature T,  and to the structure of the material at that instant:

As already stated, the set of i quantities S_i are the state variables which describe the current micro­structural state of the materials. The set of j  quantities P_j are the material properties:: lattice parameter, atomic volume, bond energies, moduli, diffusion constants, etc.; these can be regarded as constant except when the plastic properties of different materials are to be compared (Chapter 18).

            The state variables S_i generally change as deformation progresses. A second set of equations describes their rate of change, one for each state variable:

where t is time.

            The individual components of strain-rate are recovered from eqn. (1.6) by using the associated flow rule:

or, in terms of the stress and strain-rate tensors:

where C is a constant.

            The coupled set of equations (1.6) and (1.7) are the constitutive law  for a mechanism. They can be integrated over time to give the strain after any loading history. But although we have satisfactory models for the rate-equation (eqn. (1.6)) we do not, at present, understand the evolution of structure with strain or time sufficiently well to formulate expressions for the others (those for dS_i/dt). To proceed further, we must make simplifying assumptions about the structure.

            Two alternative assumptions are used here. The first, and simplest, is the assumption of constant structure:

Then the rate-equation for  completely describes plasticity. The alternative assumption is that of steady state:

Then the internal variables (dislocation density and arrangement, grain size, etc.) no longer appear explicitly in the rate-equations because they are determined by the external variables of stress and temperature. Using eqn. (1.7) we can solve for S₁, S₂, etc., in terms of  σ_s and T, again obtaining an explicit rate-equation for .

            Either simplification reduces the constitutive law to a single equation:

since, for a given material, the properties P_j are constant and the state variables are either constant or determined by σ_s and T.  In Chapter 2 we as­semble constitutive laws, in the form of eqn. (1.12), for each of the mechanisms of deformation. At low temperatures a steady state is rarely achieved, so for the dislocation-glide mechanisms we have used a constant structure formulation: the equations describe flow at a given structure and state of work­hardening. But at high temperatures, deforming materials quickly approach a steady state, and the equations we have used are appropriate for this steady behavior.  Non-steady or transient behavior is discussed in Chapter 17, Section 17.1; and ways of normalizing the constitutive laws to include change in the material properties P_j are discussed in Chapter 18.

            It is useful to have a way of summarizing, for a given polycrystalline solid, information about the range of dominance of each of the mechanisms of plasticity, and the rates of flow they produce. One way of doing this (Ashby, 1972; Frost and Ashby, 1973; Frost, 1974) [1-3] is shown in Fig. 1.2. It is a diagram with axes of normalized stress σ_s/μ and temperature, T/T_M (where µ is the shear modulus and T_M the melting temperature). It is divided into fields which show the regions of stress and tempera­ture over which each of the deformation mechanisms is dominant. Superimposed on the fields are contours of constant strain-rate: these show the net strain-rate (due to an appropriate superposition of all the mechanisms) that a given combination of stress and temperature will produce. The map displays the relationship between the three macroscopic variables: stress as, temperature T and strain-rate . If any pair of these variables are specified, the map can be used to determine the third.

            There are, of course, other ways of presenting the same information. One is shown in Fig. 1.3: the axes are shear strain-rate and (normalized) shear stress; the contours are those of temperature. Maps like these are particularly useful in fitting isothermal data to the rate-equations, but because they do not extend to 0 K they contain less information than the first kind of map.

            A third type of map is obviously possible: one with axes of strain rate and temperature (or reciprocal temperature) with contours of constant stress (Figs. 1.4 and 1.5). We have used such plots as a way of fitting constant-stress data to the rate-equations of Chapter 2, and for examining behavior at very high strain-rates (Chapter 17, Section 17.2).

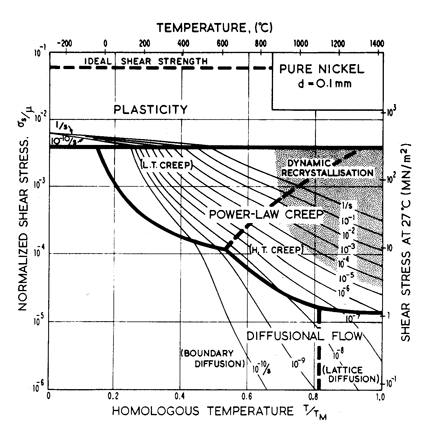
Fig. 1.2. A stress/temperature map for nominally pure nickel with a grain size of 0.1 mm. The equations and data used to construct it are described in Chapters 2 and 4.

Fig. 1.3. A strain-rate/stress map for nominally pure nickel, using the same data as Fig. 1.2.

Fig. 1.4. A strain-rate/temperature map for nominally pure nickel, using the same data as Fig. 1.2.

Fig. 1.5. A strain-rate/reciprocal temperature map for nominally pure nickel, using the same data as Fig. 1.2.

            Finally, it is possible to present maps with a structure parameter (S₁, S₂, etc.) such as dislocation density or grain size as one of the axes (see, for example, Mohamed and Langdon, 1974) [4]. Occasionally this is useful, but in general it is best to avoid the use of such microscopic structure variables as axes of maps because they cannot be externally controlled or easily or accurately measured. It is usually better to construct maps either for given, fixed values of these parameters, or for values determined by the assumption of a steady state.

Fig. 1.6. A three-dimensional map for nominally pure nickel, using the same data as Figs. 1.2, 1.3 and 1.4.

            Three of the maps shown above are orthogonal sections through the same three-dimensional space, shown in Fig. 1.6. In general, we have not found such figures useful, and throughout the rest of this book we restrict ourselves to two-dimensional maps of the kind shown in Figs. 1.2, 1.3 and, occasionally, 1.4.

            One must be careful not to attribute too much precision to the diagrams. Although they are the best we can do at present, they are far from perfect or complete. Both the equations in the following sections, and the maps constructed from them, must be regarded as a first approximation only. The maps are no better (and no worse) than the equations and data used to construct them.

References for Chapter 1