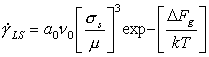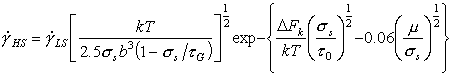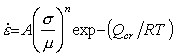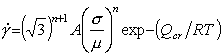ICE, H2O
16.1 General Features of the Deformation of Ice
16.2 Data for Ice
ICE IS a remarkably strong solid. When its normalized strength (σs/μ) is compared with that of other solids at the same fraction of their melting point (T/TM), ice is found to be among the strongest and hardest. In its mechanical behaviour it most closely resembles silicon and germanium (Chapter 9); but the unique character of its proton bonds (H-bonds) leads to forces opposing dislocation motion which are peculiar to ice. For this reason we compute maps for ice in two different ways: first, by treating the equations of dislocation glide and power-low creep of Chapter 2 as empirical, and fitting data for ice to them; and second, by using a set of equations for dislocation glide in ice which is based on a physical model of proton-rearrangement. The second approach is an example of glide-controlled creep and power-law breakdown (Section 2.4).
Data and maps for ice are shown in Figs. 16.1 to 16.6. They are based on data plotted in Figs. 16.1 and 16.2, and on the parameters listed in Table 16.1.
Table 16-1 Ice
|
|
Using eqns. of Ch. 2 |
|
Using eqns. of Ch. 16 |
|
|
Crystallographic and thermal data Molecular volume, Ω(m3) Burger's vector, b (m) Melting temperature, TM (K) |
3.27 x 10-29 4.52 x 10-10 273.15 |
(a) (a)
|
3.27 x 10-29 4.52 x 10-10 273.15 |
(a) (a) (a) |
|
Modulus Shear modulus at 273 K, μ0(MN/m2)
Temperature dependence of modulus, |
2.91 x 103
–0.35 |
(b)
(b) |
2.91 x 103
–0.35 |
(b)
(b) |
|
Lattice diffusion (normal) Pre-exponential, D0υ (m2/s) Activation energy, Qυ (kJ/mole) |
9.1 x 10-4 59.4 |
(c)
|
9.1 x 10-4 59.4 |
(c)
|
|
Boundary diffusion Pre-exponential, δD0b (m3/s) Activation energy, Qb. (kJ/mole) |
8.3 x 10-13 38.3 |
(d)
|
8.3 x 10-13 38.3 |
(d)
|
|
Core diffusion Pre-exponential, acD0c (m4/s) Activation energy, Qc (kJ/mole) |
3.7 x 10-22 38.3 |
(d) |
— — |
|
|
Power-law creep Exponent, n Constant, A (eqn. (16.4)) below – 8°C (s-1) Constant, A (eqn. (16.4)) above – 8°C (s-1) Activation energy below – 8°C, Qcr (kJ/mole) Activation energy below – 8°C, Qcr (kJ/mole)
|
3.0 4.32 x 1019 3.31 x 1027 80 120 |
(e)
|
— — — — — |
|
|
Lattice-resistance-controlled glide O K flow stress, Pre-exponential, Activation energy, ∆Fp/μ0b3 |
0.09 1011 0.5 |
(f)
|
— — — |
|
|
Proton rearrangement glide (eqns. (16.2) and (16.3)) Pre-exponential, a0 Proton-rearrangement frequency, v0(s-1) Reference stress τ0/μ0 Defect creation stress, τG/μ0 Activation energy for glide, ∆Fg/μ0b3 Activation energy for kink nucleation, ∆Fk/μ0b3 |
— — — — — — |
|
1.2 x 103 1.6 x 1015
0.1 0.48 0.15 |
(g) |
|
(a) Fletcher (1970]. (b) Dantl (1968); (c) Ramseier (1967); Dυ = D0υ exp – (Qυ /RT) (d) Estimated; δDb = δD0b exp – Qb/RT; acDc = acD0c exp – Qc/RT. |
e) Obtained by fitting experimental data to
eqn.(16.4). Separate sets of parameters refer to creep above and below
–8O°C. The value of A refers to tensile stress and strain rate. In
computing the maps,
(f) Obtained by fitting experimental data to eqn. (2.12). (g)Obtained by fitting experimental data to eqns. (16.2) and (16.3)—see Goodman et al., 1981. |
At atmospheric pressure, ice exists in the hexagonal lh form. The motion of dislocations in it is made difficult by a mechanism peculiar to the ice structure (Glenn, 1968) [1]. The protons which form the bridge between the oxygen ions are asymmetrically placed (Fig. 16.7) occupying one of two possible positions on each bond. The protons are disordered, even at 0 K, so that the selection of the occupied site on a given bond is random. Shear, with the protons frozen in position on the bonds, creates defects: bonds with no proton on them ("L-type Bjerrum defects") and bonds with two protons ("D-type Bjerrum defects"). With the protons randomly arranged, a defect is, on average, created on every second bond; and the
The result is that the stress required to move a dislocation in this way is very large (Glenn, 1968) [1]. If the energy absorbed, Ff per defect, is equated to the work done by the applied stress, 2σsb2a, when a length a of dislocation moves forward by 2b, one finds that the shear stress required to move a dislocation through the ice lattice with immobile protons is:
|
|
(16.1) |
At and near absolute zero, it seems probable that dislocations can move only at this high stress—for practical purposes equal to the ideal strength—and that they create many defects when they do. But at higher temperatures ice deforms plastically at stresses which are much lower than this and a dislocation must, then, move without creating such large numbers of defects. This it can do if it advances (by nucleating a kink pair) only where the local proton arrangement in its path is favourable— meaning that no defects (or an acceptably small number of defects) are created. The dislocation then drifts forward with a velocity which depends on the kinetics of proton rearrangement.
This drift velocity can be calculated (Whitworth et al., 1976 [2]; Frost et al., 1976 [3]; Goodman et al., 1981 [4]), and from it the strain-rate can be estimated. The results of such calculations suggest that, near the melting point and at low stresses, the strain-rate is determined by a linear-viscous drag caused by the sluggish rate of proton rearrangement, but that at higher stresses, kink nucleation becomes ratecontrolling. At still higher stresses, dislocations create defects as they move, and are no longer limited in their velocity by the rate of proton rearrangement. Finally at 0 K the entire resistance to glide is caused by defect-creation. An equation for the dislocation velocity, which includes this compound resistance to flow, is developed by Goodman et al. (1981) [4]. The result is that flow follows the faster of two equations. The first is dominant at low stresses, has the form of a simple power-law, with n = 3:
|
|
(16.2) |
The second is dominant at higher stresses, and includes the regime of power-law breakdown, and of low-temperature plasticity:
|
|
(16.3) |
These equations, together with the standard equations of diffusional flow, were used to construct Figs. 16.5 and 16.6. Figs. 16.1 to 16.4 were constructed using the empirical, power-law description of creep. Both are fitted to the same sets of experimental data shown in Fig. 16.1. and 16.2. The parameters extracted from this data are listed in Table 16.1.
Observations of the creep of ice in the diffusionalflow regime are confused. Bromer and Kingery (1968) [5] found behaviour consistent with Nabarro-Herring creep at σs ≈ 10-5 μ, but Butkovich and Landauer (1960) [6] and Mellor and Testa (1969) [7] who also measured creep rates at stresses near 10-5 μ, did not. Some of the confusion may be due to the contribution of transient creep (Weertman, 1969) [8]: unless the test is carried to strains exceeding 1%, transients associated with dislocation motion and grain boundary sliding may mask the true diffusional flow. And grains in ice are often large, so that rates of diffusional flow are small. But there seems no reason to suppose that diffusional flow will not occur in ice at the rate given approximately by eqn.(2.29), and that, for the appropriate regime of stress and temperature, it will appear as the dominant mechanism. This predicted regime of dominance is shown on the maps.
It is worth noting that mechanisms of flow which involve dislocation motion will create a fabric (a preferred orientation of the c-axis) in ice, but that diffusional flow will tend to destroy one. The presence or absence of fabric may—if the strains are large enough—help identify the dominant flow mechanism.
Certain other mechanisms appear in ice. Dynamic recrystallization (Section 2.4) has been observed in ice after only a few per cent strain, both in compressive creep (Steinemann, 1958) [9] and during indentation experiments (Barnes et al., 1971) [10], and almost certainly accelerates the rate of creep; the shading shows, roughly, where it occurs. Grain-boundary melting, too, accelerates creep. Barnes et al. (1971) [10] observed that creep in polycrystals (but not in single crystals) above—8°C was faster than that predicted from creep data obtained below this temperature, and that its activation energy was larger. The onset of this regime is shown by a dash-dot line on the maps. Finally, it is quite feasible that twinning can occur in ice, although we know of no direct observations of it, and it is not shown on the maps.
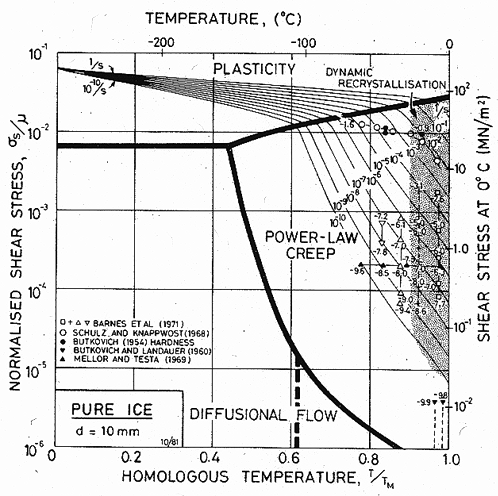
Fig. 16.1. A stress/temperature map for ice with a grain size
of 10 mm, using the empirical creep equation (eqn. (16.4)). Data are labelled
with log10 (![]() ).
).
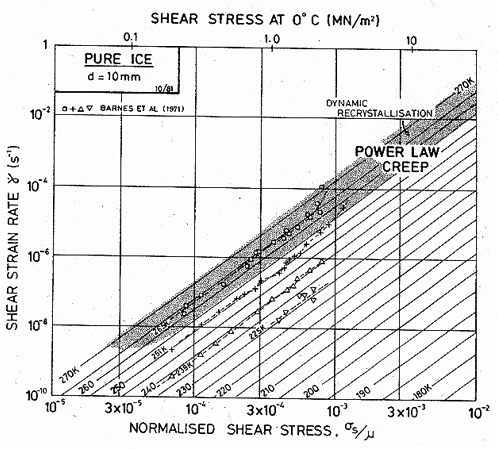
Fig. 16.2. A strain-rate/stress map for ice with a grain size of 10 mm using the empirical creep equation (eqn. (16.4)). Data are labelled with temperature in °C.
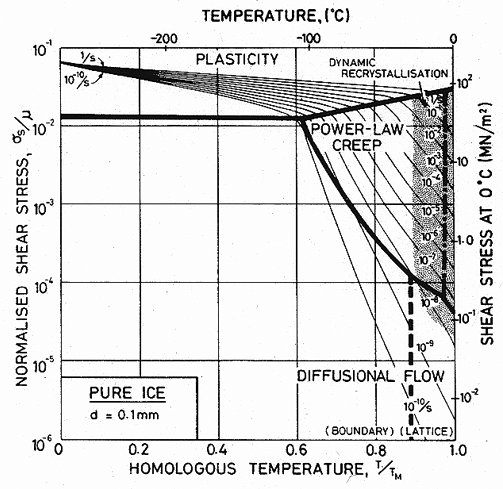
Fig. 16.3. A stress/temperature map for ice with a grain size of 0.1 mm using the empirical creep equation (eqn. (16.4)). Data are shown on Fig. 16.1.
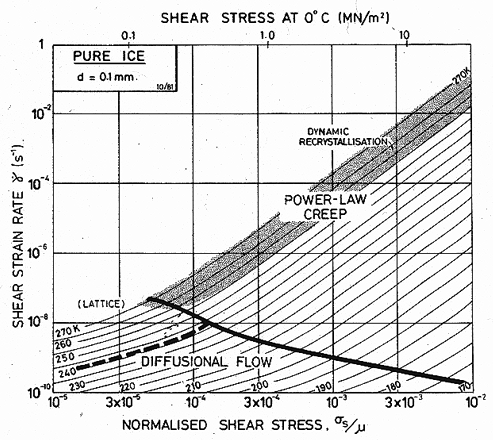
Fig. 16.4. A strain-rate/stress map for ice with a grain size of 0.1 mm using the empirical creep equation (eqn. (16.4.)). Data are shown on Fig. 16.2.
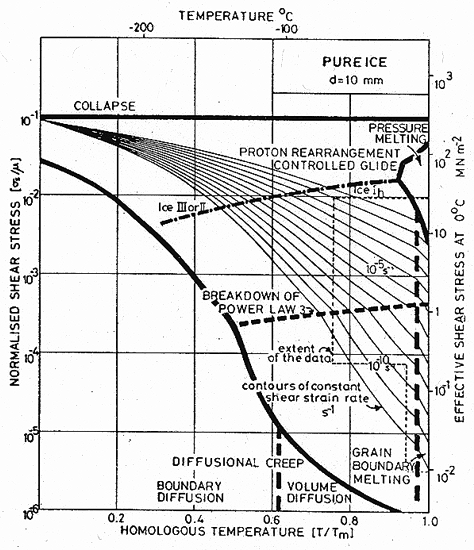
Fig. 16.5. A stress/temperature map for ice of grain size 10 mm, using the model-based equations (eqns. (16.2) and (16.3)) (Goodman et al., 1981 [4]; courtesy Phil. Mag.).
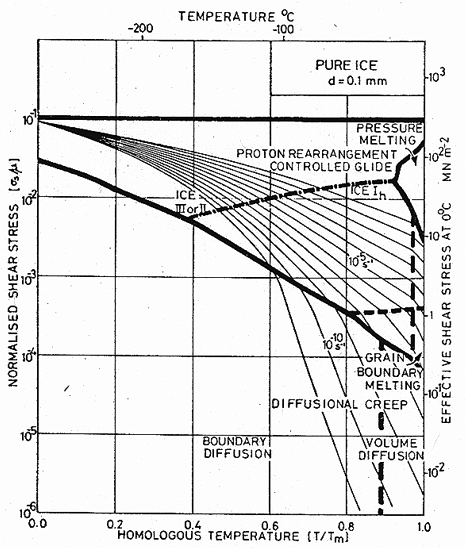
Fig. 16.6. A stress/temperature map for ice of grain size 0.1 mm, using the model-based equations (eqns. (16.2) and (16.3)) (Goodman et al., 1981 [4]; courtesy Phil. Mag.).
The crystallographic and thermal data for ice are from standard sources (see, for example, Fletcher, 1970 [11]). The shear modulus and its temperature dependence were calculated from the single-crystal data of Dantl (1968) [12] using:
|
|
Ice lh
is hexagonal, and slips most readily on the basal plane in the close-packed
directions: ![]() .
This basal slip provides only two independent slip systems; non-basal
slip must occur when polycrystalline ice deforms to large strains. Etch-pit
observations (Mugurma and Higashi, 1963) [13] suggest that the most likely systems are the
prismatic
.
This basal slip provides only two independent slip systems; non-basal
slip must occur when polycrystalline ice deforms to large strains. Etch-pit
observations (Mugurma and Higashi, 1963) [13] suggest that the most likely systems are the
prismatic ![]() and
the pyramidal
and
the pyramidal ![]() ones.
Both require higher stresses to activate them than the basal system does, and
so will control the flow strength.
ones.
Both require higher stresses to activate them than the basal system does, and
so will control the flow strength.
Self-diffusion in ice has been extensively studied (for a review, see Hobbs, 1974 [14]). The measurements show that H2, H3 and O18 diffuse at almost the same rate, indicating that the H2O molecule tends to diffuse as a unit, probably by a vacancy mechanism (Ramseier, 1967) [15]. In calculating the rate of diffusional flow we have used the lattice-diffusion coefficients of Ramseier (1967) [15] and have estimated the boundary-diffusion coefficients by setting:
|
δD0b = 2b D0υ Qb = 0.6 Qυ |
though it must be recognized that this is merely a guess.
The secondary creep of polycrystalline ice has been thoroughly reviewed by Hobbs (1974) [14], Weertman (1973) [8] and Goodman et al. (1981) [4]. There exist, too, numerous studies of the creep of single crystals of ice (see Hobbs, 1974 [14], for a review). They differ from those of polycrystalline material because easy slip occurs on the basal plane, and because large changes in the dislocation density usually take place near the beginning of the test, leading to a yield drop (in a tensile test) or a long inverse transient (in creep).
Selected data for ice are shown on Figs. 16.1 and 16.2. They serve to emphasize that creep has been studied only over a limited range of temperature, close to its melting point (0.8 to 1.0 T/TM; – 50 to 0°C). This is in contrast with creep data for other materials, little of which is obtained at such high homologous temperatures, and it is one of the reasons that ice is sometimes thought of as a weak material. This view is misleading; as the maps show, ice is surprisingly creep-resistant.
Hardness data (Atkins et
al., 1966 [16]; Tabor, 1970 [17]) have been included in Fig. 16.1. The indent
size in a creeping solid depends on the loading time as well as the indentation
pressure p, and and can be related to the creep properties of the
material beneath the indenter. We assume (following Tabor, 1951 [18]) that the mean strain beneath the indenter is about
8%, and calculate the effective shear strain-rate as 0.08 ![]() (where t
is the loading time) and the effective shear stress as
(where t
is the loading time) and the effective shear stress as ![]() .
.
The activation energy for the creep of ice differs from that for diffusion, so that the standard powerlaw creep equation (eqn. (2.21)) is inapplicable. When this is so, we use, instead, the equation:
|
|
(16.4) |
or, equivalently,
|
|
(16.5) |
(see also Chapter 7, MAR-M200).
Here ![]() and
σ are the tensile strain-rate
and stress, and Qcr, is the activation energy for creep.
Data for ice below
σs = 2 x 10-4 μ (1 MN/m2) fit this
equation well, with n = 3, provided two activation energies and two
values of A are used, one pair to describe creep below –8°C, the other
above. Above
σs =
2 x 10-4 μ the power-law breaks down,
partly because, in simple compression, cracking starts to interfere with steady
creep, and partly because of a transition to low-temperature plasticity
(Barnes et al., 1971 [10]; Section 2.4).
and
σ are the tensile strain-rate
and stress, and Qcr, is the activation energy for creep.
Data for ice below
σs = 2 x 10-4 μ (1 MN/m2) fit this
equation well, with n = 3, provided two activation energies and two
values of A are used, one pair to describe creep below –8°C, the other
above. Above
σs =
2 x 10-4 μ the power-law breaks down,
partly because, in simple compression, cracking starts to interfere with steady
creep, and partly because of a transition to low-temperature plasticity
(Barnes et al., 1971 [10]; Section 2.4).
We have fitted the creep data both to the protonrearrangement controlled glide equations (eqns. (16.2) and (16.3)) which are based on a model of dislocation motion, and to the empirical equation (eqn. (16.4)), using separate creep laws below and above –8°C. The resulting parameters are given in the two columns of Table 16.1.
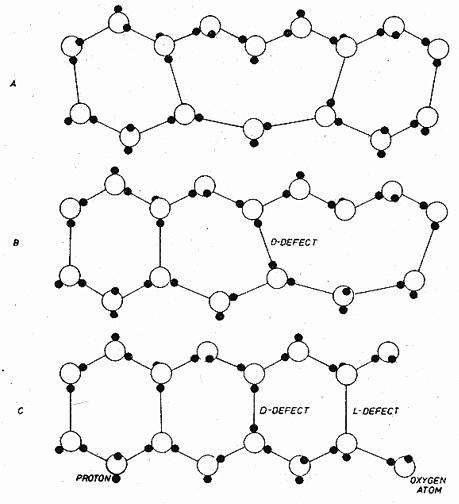
Fig. 16.7. The proton structure of ice, showing a dislocation and defects caused by its motion.
1. Glenn, J.W., Phys. Kondens. Mat., 1968. 7: p. 43.
2. Whitworth, R.W., J.G. Paren, and J.W. Glenn, The velocity of dislocations in ice: a theory based on proton disorder. Philosophical Magazine( before 1978), 1976. 33: p. 409-26.
3. Frost, H.J., D.J. Goodman, and M.F. Ashby, Kink velocities on dislocation in ice: A comment on the Whitworth, Paren and Glen Model. Philosophical Magazine, 1976. 33: p. 951-61.
4. Goodman, D.J., H.J. Frost, and M.F. Ashby, The plasticity of polycrystalline ice. Phil. Mag., 1981. 43: p. 665-95.
5. Bromer, D.J. and W.D. Kingery, Flow of polycrystalline ice at low stresses and small strains. Journal of Applied Physics, 1968. 39: p. 1688-91.
6. Butkovich, T.R. and J.K. Landauer, Snow, Ice and Permafrost Establishment Research Report , p.1. 1960.
7. Mellor, M. and R. Testa, Journal of Glaciology, 1969b. 8(147).
8. Weertman, J., Journal of Glaciology, 1969. 8: p. 494.
9. Steinemann, V.S., Beitrage zur Geologie der Schwiez, Hydrologie Nr. 10 p.1. 1958?
10. Barnes, P., D. Tabor, and J.C.F. Walker. The friction and creep of polycrystaline ice. 1971. London: Proc. R. Soc. Lond.
11. Fletcher, N.H., The Chemical Physics of Ice. 1970: Cambridge University Press. (Cambridge Monographs on Physics).
12. Dantl, G., Phys. Kondens. Mat, 1968. 7: p. 390.
13. Mugurma, J. and A. Higashi, J. Phys. Soc. Japan, 1963. 18: p. 1261.
14. Hobbs, P.V., Ice Physics. 1974, Oxford: Clarendon Press.
15. Ramseier, R.O., self-diffusion of titanium in natural and synthetic ice monocrystals. J. Appl. Phys., 1967. 38: p. 2553-56.
16. Atkins, A.G., A. Silvério, and D. Tabor, J. Inst. Met., 1966. 94: p. 369.
17. Tabor, D., The Hardness of Solids, Reviews in Physics and Technology. 1970? 1((3)): p. 145.
18. Tabor, D., The Hardness of Metals. 1951: Oxford University Press.
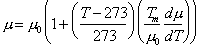 .
.