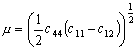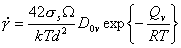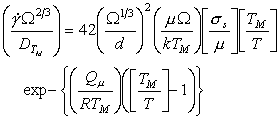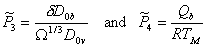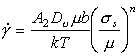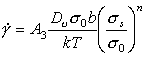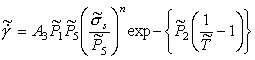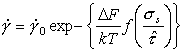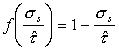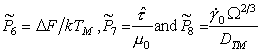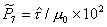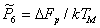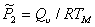CHAPTER 18

---

 SCALING LAWS AND ISOMECHANICAL GROUPS

 

18.1 The Normalization of Mechanical Data

18.2 Empirical Normalization of Data

18.3 Normalization of Constitutive Laws

18.4 Isomechanical Groups

18.5 Summary and Applications

References for Chapter 18

 

 

AN INESCAPABLE conclusion of Chapters 4 to 16 is that materials with the same crystal structure and similar bonding have similar deformation­mechanism diagrams.  When plotted on the normalized axes σ_s/μ and T/T_M, the maps for all f.c.c. metals, each fitted to experimental data, have an almost identical disposition of fields and of strain‑rate contours.  Further, they are clearly differentiated from the b.c.c. metals, or the alkali halides, or the various classes of oxides, each of which has its own characteristic map.

            Polycrystalline solids, then, can be classified into isomechanical groups by properly normalizing the data for them; the members of one group have similar mechanical properties, and are differentiated by the normalization from members of other groups.  We now examine how best to normalize data to bring out the similarities and differences between materials.  From this we derive the preliminary classification of materials into isomechanical groups given in Table 18.1.

 

TABLE 18.1 Isomechanlcal groups

 

 

 

18.1 THE NORMALIZATION OF MECHANICAL DATA

<Back to Top>

 

 

The maps of this book are plotted on normalized axes of σ_s and T/T_M.  This is a common choice for presenting mechanical data; but what are the grounds for selecting it?  There are two complementary ways to study the problem of revealing the intrinsic similarities and differences between groups of materials.  First, a purely empirical approach: if the data for a group of materials, when normalized, are brought onto a single master curve, and separated in this way from data for other groups of materials, then the normalization is a successful one.  We examine this approach in Section 18.2.  Second, a method using the model‑based constitutive laws: if a constitutive law is to be normalized such that data for a group of materials in the same structural state lie on a single master curve, then certain dimensionless combinations of material properties must be constant for that group.  This approach, which gives a basis for dividing materials into iso­mechanical groups, is developed in Section 18.3.

             Let the normalizing parameter for stress be called σ*, that for temperature T*, and that for strain­rate   There are three obvious groups of normalizing stresses σ* (Table 18.2).  The first are moduli, suggested by dislocation theory: shear moduli μ, Young's modulus E, and the bulk modulus K (because dislocation energies and line tensions depend on these).  The second are based on energies and are suggested by microscopic models for the lattice resistance and for diffusion: the cohesive energy ∆H_c, the energy of fusion ∆H_f and the energy of sublimation ∆H_υap, each divided by the atomic or molecular volume, Ω, so that σ* = ∆H_c/Ω, etc.  Finally, there are normalizing parameters based on temperatures: σ* = kT_M/Ω where k is Boltzmann's constant and Ω is the atomic or molecular volume.  The boiling point T_B and the Debye temperatures T_θ can also be treated in this way.

            Table 18.2 also lists normalizing parameters T* for temperature: they, too, can be based on the same three groups of material property used with stress, although, of course, the normalizing temperature must have the dimensions of temperature.  First there are temperatures: T_M, T_B and T_θ.  Then there are temperatures based on energy divided by the gas constant: ∆H_c/k, for example. Finally there are temperatures based on moduli: μΩ/k, for instance.

            The normalization of the strain‑rate is less obvious.  In Section 18.3 a natural normalization appears: it is  where  is the melting point diffusivity and Ω the atomic or molecular volume. It will be justified later.

            The idea of normalizing mechanical data is not new.  Dorn (1957) [1], McLean and Hale (1961) [2], Bird et al. (1969) [3], Sherby and Burke (1967) [4], Kocks et al. (1975) [5], Sherby and Armstrong (1971) [6] and Chin et al. (1972) [7] advocate, variously, the use of μ, E and c₄₄ to normalize flow stress and hardness.  The melting point, T_M, is widely used as a normalizing parameter for temperature (Sherby and Simnad, 1961 [8]; Sherby and Burke, 1967 [4]) although without convincing physical just)fication; by contrast, there are good physical grounds for using μΩ/k (Kocks et al., 1975) [5].  The normalization  (where D is the lattice diffusion coefficient) has been suggested for strain­rate (Sherby and Burke, 1967) [9], although this quan­tity is not dimensionless. Ashby and Frost (1975) [10] use instead the dimensionless quantity , as we do here.

            There have, then, been numerous attempts at normalization.  But only one systematic study has been undertaken: that reported by Brown (1980) [11] and Ashby and Brown (1981) [12].  In the rest of this chapter we follow their approach, and examine the success or failure of applying the normalizing parameters of Table 18.2, in the two ways described earlier.

 

TABLE 18.2 Normalizing parameters

k  = Boltzmann's constant

Ω = Atomic or molecular volume

 

 

18.2 EMPIRICAL NORMALIZATION OF DATA

<Back to Top>

 

           The maps of this book are based on experimental data, much of which are plotted on the maps themselves or on separate data plots.  The striking similarity between the data plots for the b.c.c. transition metals of Chapter 5, for instance, confirms that the normalization σ_s/μ and T/T_M has some merit in revealing intrinsic similarities and differences between materials.  But the data on these plots derive from many different investigators each applying different techniques to samples of differing purity; the inevitable scatter makes it hard to distinguish between alternative normalizations.

            To avoid this, Brown (1980) [11] and Ashby and Brown (1981) [12] measured the Vickers hardness H (MN/m²) of single crystals of some 25 elements and compounds, forming seven distinct groups, over a wide range of temperature.  The samples were, as nearly as possible, in a standard state of purity and history.  Fig. 18.1 shows an example: in it, the hardnesses of nine alkali halides are plotted against temperature from 88 K to about 1000 K.  At a given temperature, the hardness range is about a factor of 35.

            Ashby and Brown then investigate the effect of normalizing these data in the various ways listed in Table 18.2.  The data for each group of materials were replotted on normalized axes, a curve fitted to them, and the mean square deviation from the curve was used to measure the success of the normalization.  Fig.18.2 shows the data for the alkali halides after the normalization H/μ and T/T_M.

            Some normalizations for the temperature are not successful.  Normalizing by the Debye temperature T_θ (to form T/T_θ), for example, increases the spread of the data.  In every case the best correlation is given by normalizing temperature by the melting point, T_M, although the use of EΩ/k or μΩ/k (where Ω is the atomic or molecular volume) is almost as good.  This is because the normalizing parameters are not independent.  In particular, the moduli and the melting point are correlated for many elements and compounds.  Fig. 18.3 shows the correlation which, to a good approximation, is described by: 

(18.1)

and

(18.2)

(where E₀ and μ₀ are the values of E and μ at 300 K).  This is important, since models for plasticity (Kocks et al., 1975 [5]) suggest the normalization kT/μΩ rather than T/T_M for temperature.  The correlation makes T_M an acceptable substitute for μΩ/k, and an exceedingly convenient one, since the range for which the material is solid is then spanned by range 0 < T/T_M < 1.

            The best normalization for the stress or the hardness is by the cohesive energy (∆H_c/Ω).  Applying it to the data for the alkali halides gives a scatter, as measured by a correlation coefficient, which is only slightly greater than that within data for a single alkali halide.  Certain other normalizations are almost as good. For cubic materials, normalization by   works tolerably well.  Normalization by a mean Young's modulus is better and has the advantage that only the bare minimum of data (E, T_M) are necessary to perform it.  The cohesive energy, despite its good performance, is not attractive for general use: it is hard to measure, and is not known for many compounds for which mechanical data exist; a modulus, though slightly less good, is much more convenient.  We chose to use μ because dislocation theory suggests that, in many cases, strength should scale as the line energy of a glide dislocation, and (for a screw) this is a proportional to μ.

            When data for groups of oxides and of elements are analysed in the same way, it is again found that the normalizations by μ and T_M (or by E and T_M) bring the hardnesses of members of one group onto a single master curve and distinguish them from those of other groups.  This success suggests a less laborious way of identifying isomechanical groups.  It is discussed in the next section.

 

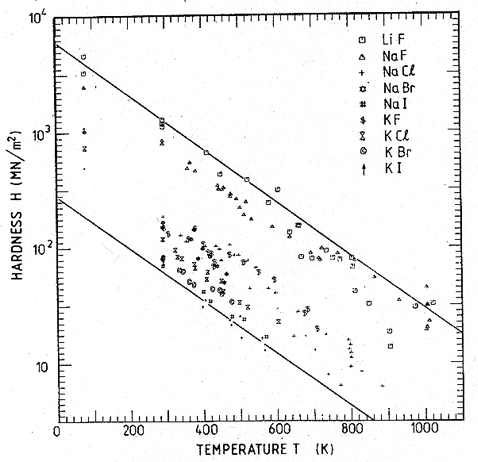
Fig.18.1. The Vicker's hardness H of nine alkali halides in, as nearly as possible, the same structural state, plotted against temperature.

 

 

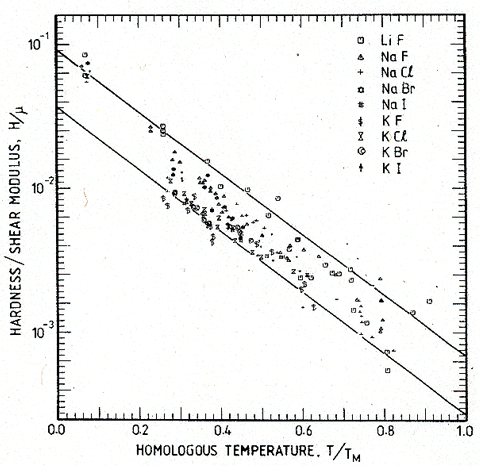
Fig.18.2. The data of Fig.18.1, replotted on the normalized axes H/μ and T/T_M. The spread of data is reduced from a factor of 25 to a factor of 2.5. A plot on axes of HΩ/∆H_c and T/T_M is even more successful, but less convenient to use.

 

 

Fig. 18.3. The correlation between the melting temperatures and Young's moduli and the shear moduli of polycrystals.

 

 

18.3 NORMALIZATION OF CONSTITUTIVE LAWS

<Back to Top>

 

Chapter 2 described simple models for the mechanism of plastic flow. Each mechanism was described by a constitutive law of the form (Chapter 1, eqn. (1.1)): 

(18.3)

Here, it will be remembered, S_i is a set of state variables which describe the microstructural state of the materials (its dislocation density, grain size, cell size, etc.) and P_j is a set of material properties (bond energies, moduli, diffusion constants, and so forth) which are constant for a given material, but, of course, differ from one material to another.

            If we choose a set of normalizing parameters, σ*, T*, *, with the dimensions of stress, temperature and strain rate, the constitutive law can be written: 

where

(18.5)

The quantities  and  are normalized, dimensionless state variables and material properties.  It now follows that if the normalizing parameters, σ*, T* and  bring together data from a given group of materials, in an equivalent microstructural state ( the same), thereby causing them to lie on a single master curve: 

(18.6)

then the dimensionless material properties  must be constants for the members of that group.

            The approach is most easily understood through an example.  At high temperatures and low stresses, diffusional flow can become the dominant deformation mechanism (Chapter 2, Section 2.5).  When lattice diffusion limits the creep rate, this rate (eqn. (2.29)) is given by: 

(18.7)

This equation has the form of eqn. (18.3): it relates the macroscopic variables (, σ_s, T) to the structure (the grain size, d ) and to material properties (atomic volume, Ω, and lattice diffusion constants D_0υ and Q_υ).  Normalizing by μ and T_M gives: 

(18.8)

or

(18.9)

where .  Here DT_M, is the diffusion coefficient at the melting point and the strain‑rate has been normalized by  to give .  The normalized stress is  and normalized temperature is .

            This is a relationship between , and T and .  Members of a group of materials, in the same micro­structural state , now have coincident diffusional creep behaviour if the properties  and  are constants for that group.  So we obtain a second, quite separate, indicator of a good choice of normalizing parameter by examining how nearly constant the quantities  and  are.

            They are plotted in Figs.18.4 and 18.5 (data from standard sources; see also Brown and Ashby, 1980a [13]).  The value of each, for a given group of materials, has a narrow range, and the values for different groups are distinct.  In addition, the normalizing parameter  (which measured the atomic jump frequency at the melting point) is shown in Fig. 18.6.  It, too, has a characteristic value for each group.

            Diffusional flow may involve boundary diffusion also.  If the full constitutive law (eqn. (2.29) with eqn. (2.30)) is normalized as before, two new material parameters appear: 

where D_0υ and D_0b are the pre‑exponentials for each diffusion path and Q_b is the activation energy for boundary diffusion.  Data are available for some 15 materials, but they are inadequate to construct plots like Figs. 18.4 and 18.5.  Instead we tabulate the parameter  and the ratio  (Table 18.3; data from Brown and Ashby, 1980a [13]).  Both are roughly constant.  As with  and , each group of materials has characteristic values of  and , which distinguish it from the other groups.

            A similar procedure can be applied to power‑law creep (Chapter 2, Section 2.4).  At high temperatures, creep is frequently (though not always) limited by lattice diffusion.  Then (eqn. (2.21)) its rate is: 

(18.10)

This is the most difficult constitutive law with which to deal because, although the creep exponent n is roughly constant for pure elements and compounds (generally n = 4 ± 1), the creep "constant" A varies by many orders of magnitude.  This difficulty with the creep equation has been examined by Brown and Ashby (1980b) [14] who rewrite the equation as: 

where σ₀  is a material property.  When σ₀ is properly defined it is found to be approximately constant for a given class of material; and with this value of σ₀ , the dimensionless quantity A₃ is a constant also (its value is approximately 1.6 x 10^‑6).

            Normalizing by σ₀  and T_M gives: 

(18.11)

where (as before) ,  and  and  and  were defined earlier.  Although the equation contains three dimensionless material properties, only one is new: it is the quantity .  Reliable data for it are sparse; the best estimates we can make are given in Table 18.3 (Brown and Ashby, 1980b [14]).

            Finally, low‑temperature plasticity (Chapter 2, Section 2.2) is described by a rate equation of the general form: 

(18.12)

Here ∆F is the activation energy for glide, for either lattice‑resistance or obstacle control.  The pre­exponential  has the dimensions of strain‑rate, and , the flow strength at 0 K, has the dimensions of stress.  The function f is unimportant; it is commonly of the form: 

Normalizing by (μ, T_M) as before, leads to three new dimensionless properties: 

Their approximate values for various material groups, for lattice‑resistance controlled glide, are given in Table 18.3.

 

 

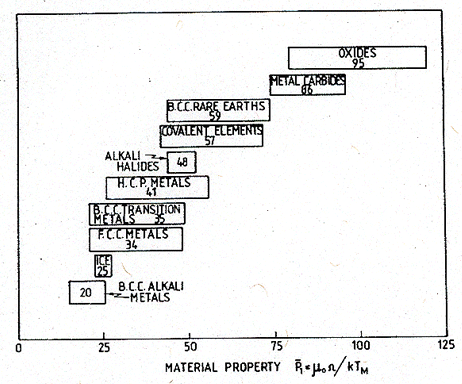
Fig. 18.4. The ranges of the dimensionless quantity μ₀Ω/kT_M for classes of solids.

 

 

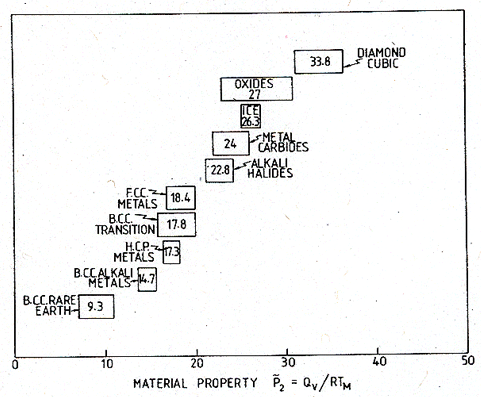
Fig. 18.5. The ranges of the dimensionless quantity Q_υ/RT_M for classes of solids.

 

 

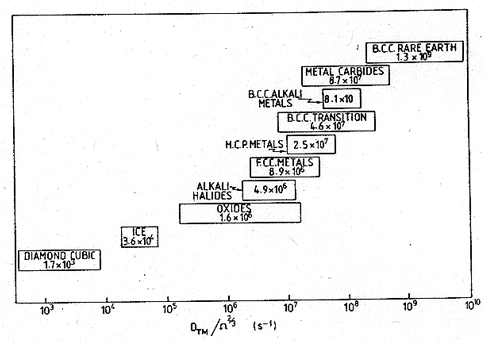
Fig. 18.6. The ranges of the quantity (s^-1) for classes of solids.

 

 

 18.4 ISOMECHANICAL GROUPS

 

            Both the investigation of scaling (Sections 18.2 and 18.3) suggest that materials can be classified into isomechanical groups.  The members of a group are mechanically similar, and by proper scaling their mechanical properties can be brought, more or less, into coincidence.  The same scaling separates and distinguishes this group from other groups.

            The f.c.c. metals form an isomechanical group. So, too, do the diamond cubic elements.  But it is not just the structure which determines mech­anical strength.  Rock‑salt structured materials, for example, fall into four separate mechanical groups (Table 18.1).  The tonically bonded alkali halides form one such group.  But they are quite distinct from the transition‑metal carbides and from the rock‑salt structured oxides; and in ways that do not relate simply to the modulus and the melting point.  The b.c.c. metals provide a second example.  The data plotted in Figs.18.4, 18.5 and 18.6 show a clear differentiation into three isomechanical groups: the alkali metals, the transition metals and the lanthanides.

            It is necessary, then, to divide materials accord­ing to both structure and bonding if mechanical behaviour is to be grouped.  But the groups are still large ones.  A first attempt at this classification for elements and simple compounds is shown in Table 18.1.

 

 

18.5 SUMMARY AND APPLICATIONS

<Back to Top>

  

            The systematic examination of scaling relations for mechanical behaviour summarized above shows that when stress, temperature and strain‑rate are appropriately normalized, materials of the same structure and bonding, in the same microstructural state (grain size, purity, state of work‑hardening and so forth) can be described by a single master­diagram.  Successful normalizations bring data for members of a given isomechanical group together, and distinguish them from other groups.

            This is because, in the broadest sense, mechanical behaviour is governed by a set of dimensionless material properties . The values of  are essentially constant for each isomechanical group—meaning solids with the same structure and similar bonding.  The most successful normalization for σ, T and  is that described by (∆H_c/Ω, T_M, DT_M/Ω^2/3), but the normalizations (μ, T_M, DT_M/Ω^2/3)  or (E, T_M, DT_M/Ω^2/3) are almost as good, and much more convenient.

 

 TABLE 18.4 Progression of material properties

 

 

            The results have certain applications.  First they allow one to see, at a very simple level, how classes of solids differ, and how the differences arise  There is a steady progression in the mechanical behaviour as the bonding becomes increasingly localized because this (i) generates an increasing lattice resist­ance, and (ii) raises the activation energy for both glide and for diffusion.  Table 18.4 summarizes this progression.  Note the increasing values of ,  and  as the bonding changes from metallic to ionic and covalent.  It may be objected that material properties such as the stacking fault energy of f.c.c. crystals, or the c/a ratio of hexagonal crystals, or the stoichiometry of oxides, have been neglected in this treatment—and it is true that they have a considerable influence on a mechanical behaviour.  But we are concerned here with the gross differences between broad classes of solids (the differences between b.c.c. metals and diamond cubic elements, for instance) and on this gross scale it is the quantities tabulated here which determine the characteristics of mechanical behaviour.  Such quantities as stacking fault energy produce smaller variations about these characteristic or baseline properties.

            The existence of such isomechanical groups also means that, at an approximate level, the mechanical behaviour can be predicted.  Such a need appears in geology and geophysics, and (less often) in materials science and applied physics.  Then data for one member of an isomechanical group can be scaled to give some idea of the behaviour of other, less well‑characterized members of the group, provided its modulus and melting point are known.  The maps shown in Chapters 4 to 16 can be thought of as typifying the group of solid to which they belong.  Thus an approximate but useful description of the behaviour of (for instance) gold can be obtained from the map for copper or nickel, using the normalized axes (Chapter 4); an approximate description of NaI can be obtained from the map for NaCl (Chapter 10); and the mechanical behaviour of PuO₂ should be well approximated by that for UO₂ (Chapter 13).

 

 

References for Chapter 18

<Back to Top>

 

1.         Dorn, J.E., Creep and Recovery. 1957: ASM, Ohio. 2255.

2.         McLean, D. and K.F. Hale, Structural Processes in Creep. 1961, London: Iron and Steel Institute. 86.

3.         Bird, J.E., A.K. Mukherjee, and J.F. Dorn, Correlations Between High-Temperature Creep Behaviour and Structure, D.G.a.R. Brandon, A., Editor. 1969, Haifa University Press, Israel. p. 255-341.

4.         Sherby, O.D. and P.M. Burke, Mechanical behavior of crystalline solids at elevated temperature. Prog. Mat. Sci., 1967. 13: p. 325.

5.         Kocks, U.F., A.S. Argon, and M.F. Ashby, Prog. Mat. Sci., 1975. 19: p. 1.

6.         Sherby, O.D. and P.E. Armstrong, Prediction of activation energies for creep and self-diffusion from hot hardness data. Met. Trans., 1971. 2: p. 3479.

7.         Chin, G.Y., et al., Hardness, yield strength and young's modulus in halide crystals. Scripta Metallurgica, 1972. 6: p. 475-80.

8.         Sherby, O.D. and M.T. Simnad, Prediction of atomic mobility in metallic systems. Trans. ASM., 1961. 54: p. 227.

9.         Sherby, O.D. and P.M. Burke, Prog. Mat. Sci., 1967. 13: p. 1.

10.       Ashby, M.F. and H.J. Frost, eds. Constitutive Relations in Plasticity. ed. A. Argon. 1975, MIT Press. 116.

11.       Brown, A.M., The Temperature Dependence of the Vickers Hardness of Isostructural Compounds. 1980, University of Cambridge.

12.       Ashby, M.F. and A.M. Brown. On Deformation of polycrystals. in Proc. 2nd RisØ Int. Symp. on the Deformation of Polycrystals. 1981.

13.       Brown, A.M. and M.F. Ashby, Correlations for diffusion constants. Acta Metallurgica (pre 1990), 1980a. 28: p. 1085.

14.       Brown, A.M. and M.F. Ashby, On the power-law creep equation. Scripta Metallurgica (before 1990), 1980b. 14: p. 1297.