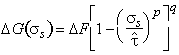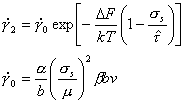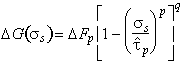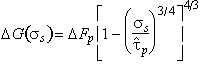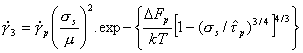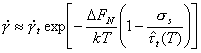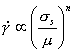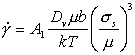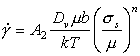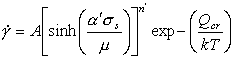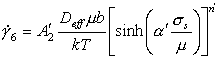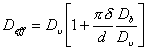RATE-EQUATIONS
2.1 Elastic Collapse
2.2 Low-Temperature Plasticity: Dislocation Glide
2.4 High-Temperature Plasticity: Power-Law Creep
2.5 Diffusional Flow
IN THIS chapter we develop, with a brief explanation, the rate-equations used later to construct the maps. We have tried to select, for each mechanism, the simplest equation which is based on a physically sound microscopic model, or family of models. Frequently this equation contains coefficients or exponents for which only bounds are known; the model is too imprecise, or the family of models too broad, to predict exact values. Theory gives the form of the equation; but experimental data are necessary to set the constants which enter it. This approach of “model-based phenomenology” is a fruitful one when dealing with phenomena like plasticity, which are too complicated to model exactly. One particular advantage is that an equation obtained in this way can with justification (since it is based on a physical model) be extrapolated beyond the range of the data, whereas a purely empirical equation cannot.
In accordance with this approach we have aimed at a precision which corresponds with the general accuracy of experiments, which is about ±10% for the yield strength (at given T and δ, and state of work-hardening), or by a factor of two for strainrate at given σs and T ). For this reason we have included the temperature-dependence of the elastic moduli but have ignored that of the atomic volume and the Burgers' vector.
Pressure is not treated as a variable in this chapter. The influence of pressure on each mechanism is discussed, with data, in Chapter 17, Section 17.4.
The equations used to construct the maps of later chapters are indicated in a box. Symbols are defined where they first appear in the text, and in the table on pages ix to xi.
The ideal shear strength defines a stress level above which deformation of a perfect crystal (or of one in which all defects are pinned) ceases to be elastic and becomes catastrophic: the crystal structure becomes mechanically unstable. The instability condition, and hence the ideal strength at 0 K, can be calculated from the crystal structure and an inter-atomic force law by simple statics (Tyson, 1966; Kelly, 1966) [1, 2]. Above 0 K the problem becomes a kinetic one: that of calculating the frequency at which dislocation loops nucleate and expand in an initially defect-free crystal. We have ignored the kinetic problem and assumed the temperaturedependence of the ideal strength to be the same as that of the shear modulus, μ, of the polycrystal. Plastic flow by collapse of the crystal structure can then be described by:
|
|
(2.1) |
Computations of α lead to values between 0.05 and 0.1, depending on the crystal structure and the force law, and on the instability criterion. For the f.c.c. metals we have used α = 0.06, from the computer calculations of Tyson (1966) [1] based on a Lennard-Jones potential. For b.c.c. metals we have used α = 0.1, from the analytical calculation of MacKenzie (1959) [3]. For all other materials we have used α =0.1.
Below
the ideal shear strength, flow by the conservative, or glide, motion of
dislocations is possible—provided (since we are here concerned with polycrystals)
an adequate number of independent slip systems is available (Figs. 2.1 and
2.2). This motion is almost always obstacle-limited: it is the
interaction of potentially mobile dislocations with other dislocations, with
solute or precipitates, with grain boundaries, or with the periodic friction
of the lattice itself which determines the rate of flow, and (at a given rate)
the
yield strength. The yield strength of many polycrystalline materials does not
depend strongly on the rate of straining—a fact which has led to models for
yielding which ignore the effect of strain-rate (and of temperature)
entirely. But this is misleading: dislocation glide is a kinetic process. A
density ρm of
mobile dislocations, moving through a field of obstacles with an average
velocity 
determined
almost entirely by their waiting time at obstacles, produces a strain-rate
(Orowan, 1940) [4] of:
|
|
(2.2) |
where b is the magnitude of the Burgers' vector of the dislocation. At steady state, ρm, is a function of stress and temperature only. The simplest function, and one consistent with both theory (Argon, 1970) [5] and experiment is:
|
|
(2.3) |
where
α is a constant of
order unity. The velocity depends on the force
F = σsb acting,
per unit length, on the dislocation, and on its mobility, M :
|
|
(2.4) |
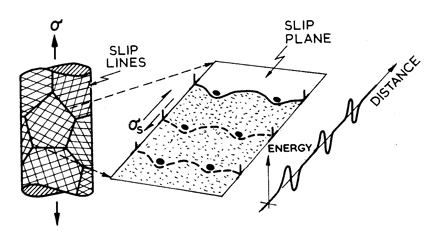
Fig. 2.1. Low-temperature plasticity limited by discrete obstacles. The strain-rate is determined by the kinetics of obstacle cutting.
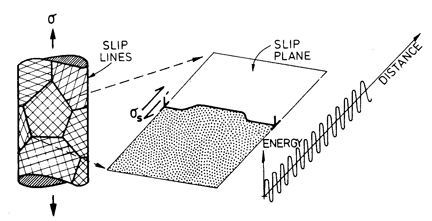
Fig. 2.2. Low-temperature plasticity limited by a lattice resistance. The strain-rate is determined by the kinetics of kink nucleation and propagation.
The
kinetic problem is to calculate M, and thus
. In the most interesting
range of stress, M is determined by the rate at which dislocation
segments are thermally activated through, or round, obstacles. In developing
rate-equations for low-temperature plasticity (for reviews, see
Evans and Rawlings, 1969; Kocks et al., 1975; de Meester et al., 1973)
[6-8] one immediately encounters a difficulty: the velocity is always an exponential function of stress, but the details of the exponent depend on the shape and nature of the obstacles. At first sight there are as many rate-equations as there are types of obstacle. But on closer examination, obstacles fall into two broad classes: discrete obstacles which are bypassed individually by a moving dislocation (strong dispersoids or precipitates, for example) or cut by it (such as forest dislocations or weak precipitates); and extended, diffuse barriers to dislocation motion which are overcome collectively (a lattice-friction, or a concentrated solid solution). The approach we have used is to select the rate-equation which most nearly describes a given class of obstacles, and to treat certain of the parameters which appear in it as adjustable, to be matched with experiment. This utilizes the most that model-based theory has to offer, while still ensuring an accurate description of experimental data.
The
velocity of dislocations in a polycrystal is frequently determined by the
strength and density of the discrete obstacles it contains (Fig. 2.1).
If the Gibbs free-energy of activation for the cutting or by-passing
of an obstacle is ∆G(σs), the mean velocity of a dislocation
segment, ,
is given by the kinetic equation (see reviews listed above):
|
|
(2.5) |
where
β, is a
dimensionless constant, b is the magnitude of the Burgers'
vector, and is
a frequency.
The quantity ∆G(σs) depends on the distribution of obstacles and on the pattern of internal stress, or “shape”, which characterizes one of them. A regular array of box-shaped obstacles (each one viewed as a circular patch of constant, adverse, internal stress) leads to the simple result:
|
|
(2.6) |
where ∆F is the total free energy (the activation energy) required to
overcome the obstacle without aid from external stress. The material property
is the stress
which reduced ∆G to zero, forcing the dislocation through the obstacle
with no help from thermal energy. It can be thought of as the flow strength of
the solid at 0 K.
But obstacles are seldom box-shaped and regularly spaced. If other obstacles are considered, and allowance is made for a random, rather than a regular, distribution, all the results can be described by the general equation (Kocks et al., 1975) [7]:
|
|
(2.7) |
The quantities p, q and ∆F are bounded: all models lead to values of
|
|
(2.8) |
The importance of p and q depends on the magnitude of ∆F. When ∆F is large, their influence is small, and the choice is unimportant; for discrete obstacles, we use p = q = 1. But when ∆F is small, the choice of p and q becomes more critical; for diffuse obstacles we use values derived by fitting data to eqn.(2.7) in the way described in the next sub-section.
The strain rate sensitivity of the strength is determined by the activation energy ∆F—it characterizes the strength of a single obstacle. It is helpful to class obstacles by their strength, as shown in Table 2.1; for strong obstacles ∆F is about 2μb3 for weak, as low as 0.05μb3. A value of ∆F is listed in the Tables of Data for each of the materials analysed in this book. When dealing with pure metals and ceramics in the work-hardened state, we have used ∆F= 0.5 μb3.
The
quantity is
the "athermal flow strength"— the shear strength in the absence of
thermal energy. It reflects not only the strength but also the density and
arrangement of the obstacles. For widely spaced, discrete obstacles,
is proportional
to μb/l where l is
the obstacle
spacing; the constant of proportionality depends on their strength and distribution
(Table 2.1). For pure metals strengthened by work-hardening we have
simply used =
μb/l (which
can be
expressed in terms of the ρ density,
of forest dislocations: 
). The Tables of Data list 
, thereby specifying
the degree of
workhardening.
If we now combine eqns (2.3), (2.4), (2.5) and (2.7) we obtain the rate-equation for discrete-obstacle controlled plasticity:
|
where |
|
(2.9) |
When ∆F is large
(as here), the stress dependence of the exponential is so large that, that of
the pre-exponential can be ignored. Then
can be treated as a constant. We have
set =
106 /s, giving a good fit
to experimental data.
Eqn. (2.9) has been used in later chapters to describe plasticity when the strength is determined by work-hardening or by a strong precipitate or dispersion; but its influence is often masked by that of a diffuse obstacle: the lattice resistance, the subject of the next section.
The velocity of a dislocation in most polycrystalline solids is limited by an additional sort of barrier: that due to its interaction with the atomic structure itself (Fig. 2.2). This Peierls force or lattice resistance reflects the fact that the energy of the dislocation fluctuates with position; the amplitude and wavelength of the fluctuations are determined by the strength and separation of the inter-atomic or intermolecular bonds. The crystal lattice presents an array of long, straight barriers to the motion of the dislocation; it advances by throwing forward kink pairs (with help from the applied stress and thermal energy) which subsequently spread apart (for reviews see Guyot and Dorn, 1967; Kocks et al., 1975) [7, 9].
It is usually the nucleation-rate of kink-pairs which limits dislocation velocity. The Gibbs free energy of activation for this event depends on the detailed way in which the dislocation energy fluctuates with distance, and on the applied stress and temperature. Like those for discrete obstacles, the activation energies for all reasonable shapes of lattice resistance form a family described (as before) by:
|
|
(2.10) |
where ∆Fp is the Helmholtz free energy of an isolated pair of
kinds and
is,
to a sufficient approximation, the flow stress at 0 K*. An analysis of
data (of which Fig. 2.3 is an example) allows p and q to be determined.
We find the best choice to be:
|
|
(2.11) |
Combining this with eqns. (2.2), (2.3) and (2.5) leads to a model-based rate-equation for plasticity limited by a lattice resistance:
|
|
(2.12) |
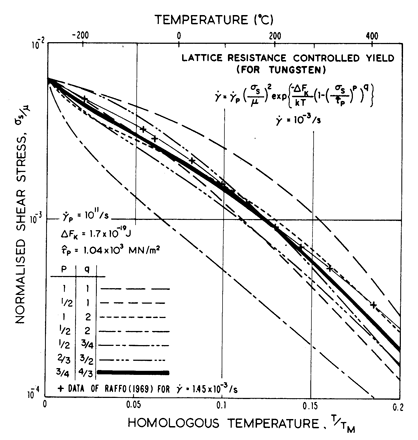
Fig. 2.3.
Predicted contours for 
= 10-3/s for various formulations of the lattice-resistance
controlled glide equation (eqn. (2.12)), compared with data for tungsten.
The influence of the choice of p and q is illustrated in Fig. 2.3. It shows how the measured strength of tungsten (Raffo, 1969) [10] varies with temperature, compared with the predictions of eqn. (2.12), with various combinations of p and q. It justifies the choice of 3/4 and 4/3, although it can be seen that certain other combinations are only slightly less good.
* The equation
of Guyot and Dorn (1967) [9] used in the earlier report (Ashby, 1972a) [11] will be recognized as the special case of p = 1, q = 2. This equation was misprinted as
instead
of
in the
paper by
Ashby (1972a).
The
pre-exponential of eqn. (2.12) contains a term in
arising from the variation
of mobile dislocation density with stress (eqn. (2.3), which must, when
∆Fp is small
(as here), be retained. In using eqn. (2.12) to describe the low-temperature
strength of the b.c.c. metals and of ceramics, we have used
= 1011/s —a mean value obtained by
fitting data to eqn. (2.12). If data allow it,
should be determined from experiment;
but its value is not nearly as critical as those of
∆Fp and
, and data of sufficient
precision to justify changing it are rarely available. With this value of
the quantities ∆Fp (typically 0.1
μb3) and
(typically
10-2 μ) are obtained by
fitting eqn. (2.12) to experimental data for the material in question. The
results of doing this are listed in the Tables of Data in following chapters.
It
should be noted that the values of
(and of
) for single
crystals and polycrystals differ. The difference is a Taylor factor: it depends
on the crystal structure
and on the slip systems which are activated when the polycrystal deforms. For
f.c.c. metals the appropriate Taylor factor Ms is 1.77; for
the b.c.c. metals it is
1.67 (Kocks, 1970) [12]. (They may be more familiar to the reader as the Taylor
factors M = 3.06 and 2.9, respectively, relating the critical resolved
shear strength to tensile strength for f.c.c. and b.c.c. metals. Since
and
are polycrystal
shear strengths, the factors we use are less by the factor
√3) For less
symmetrical
crystals the polycrystal shear strength is again a proper average of the
strengths of the active slip systems. These often differ markedly and it is reasonable
to identify for
the polycrystal with that of the hardest of the slip systems (that is, we take
Ms=1 but
use
for the
hard
system). In calculating or
from single
crystal data, we have
applied the appropriate Taylor factor.
Under conditions of explosive or shock loading, and in certain metal-forming and machining operations, the strain-rate can be large (>102/s). Then the interaction of a moving dislocation with phonons or electrons can limit its velocity. The strength of the interaction is measured by the drag coefficient, B (the reciprocal of the mobility M of eqn. (2.4)):
|
|
Values of B lie, typically, between 10-5 and 10-4 Ns/m2 (Klahn et al., 1970) [13]. Combining this with eqn. (2.4) leads to the rate-equation for drag limited glide:
|
|
(2.13) |
where c is a constant which includes the appropriate Taylor factor.
To use this result it is necessary to know how ρm/B varies with stress and temperature. For solute drag, ρm is well described by eqn. (2.3); but at the high strain-rates at which phonon drag dominates, ρm tends to a constant limiting value (Kumar et al., 1968; Kumar and Kumble, 1969) [14, 15], so that ρm/B is almost independent of stress and temperature. Then the strain-rate depends linearly on stress, and the deformation becomes (roughly) Newtonian-viscous:
|
|
(2.14) |
where C (s-1) is a constant. Using the data of Kumar et al. (1968) [14] and Kumar and Kumble (1969) [15], we estimate C ≈ 5 x 106 /s.
Drag-controlled plasticity does not appear on most of the maps in this book, which are truncated at strain-rate (1/s) below that at which it becomes important. But when high strain-rates are considered (Chapter 17, Section 17.2), it appears as a dominant mechanism.
A
solute introduces a friction-like resistance to slip. It is caused by
the interaction of the moving dislocations with stationary weak obstacles:
single solute atoms in very dilute solutions, local concentration fluctuations
in solutions which are more concentrated. Their effect can be described by eqn.
(2.9) with a larger value of and a smaller value of
∆F (Table
2.1). This effect is superimposed on that of work-hardening. In
presenting maps for alloys (Chapter 7) we have often used data for heavily
deformed solid solutions; then solution strengthening is masked by forest
hardening. This allows us to use eqn. (2.9) unchanged.
A
dispersion of strong particles of a second phase blocks the glide motion
of the dislocations. The particles in materials like SAP (aluminium
containing Al203), T-D Nickel (nickel containing
ThO2—Chapter 7), or low-alloy steels (steels containing dispersions
of carbides—Chapter 8) are strong and stable. A gliding dislocation can
move only by bowing between and by-passing them, giving a contribution
to the flow strength which scales as the reciprocal of the particle spacing,
and which has a very large activation energy (Table 2.1). Detailed calculations
of this Orowan strength (e.g. Kocks et al., 1975 [7]) lead to eqn. (2.9) with
and
∆F ≥ 2μb3. This activation
energy is so large that it leads to a flow strength which is almost athermal,
although if the alloy is worked sufficiently the yield strength will regain the
temperature-dependence which characterizes forest hardening (Table 2.1).
We have neglected here the possibility of thermally activated cross-slip
at particles (Brown and Stobbs, 1971; Hirsch and Humphreys, 1970) [16, 17], which can relax work-hardening and thus lower the flow strength. To a first approximation, a strong dispersion and a solid solution give additive contributions to the yield stress.
A precipitate,
when finely dispersed, can be cut by moving dislocations. If the density of
particles is high, then the flow strength is high (large
but strongly
temperature-dependent (low ∆F: Table 2.1). If the precipitate is
allowed to coarsen it behaves increasingly like a dispersion of strong
particles.
Twinning is an important deformation mechanism at low temperatures in h.c.p. and b.c.c. metals and some ceramics. It is less important in f.c.c. metals, only occurring at very low temperature. Twinning is a variety of dislocation glide (Section 2.2) involving the motion of partial, instead of complete, dislocations. The kinetics of the process, however, often indicate that nucleation, not propagation, determines the rate of flow. When this is so, it may still be possible to describe the strain-rate by a rate-equation for twinning, taking the form:
|
|
(2.15) |
Here
∆FN is the
activation free energy to nucleate a twin without the aid of external stress;
is a constant with
dimensions of strain-rate which includes the density of available
nucleation sites and the strain produced per successful nucleation;
is the stress
required to nucleate twinning in the absence of thermal activation. The
temperature-dependence of ∆FN must be included to explain
the observation that the twinning stress may decrease with decreasing
temperature (Bolling and Richman, 1965) [18].
The rate-equation for twinning is so uncertain that we have not included it in computing the maps shown here. Instead, we have indicated on the dataplots where twinning is observed. The tendency of f.c.c. metals to twin increases with decreasing stacking fault energy, being greatest for silver and completely absent in aluminium. All the b.c.c. and h.c.p. metals discussed below twin at sufficiently low temperature.
At high temperatures, materials show ratedependent plasticity, or creep. Of course, the mechanisms described in the previous sections lead, even at low temperatures, to a flow strength which depends to some extend on strain-rate. But above 0.3TM for pure metals, and about 0.4TM for alloys and most ceramics, this dependence on strain-rate becomes much stronger. If it is expressed by an equation of the form
|
|
(2.16) |
then, in this high-temperature regime, n has a value between 3 and 10, and (because of this) the regime is called power-law creep. In this section we consider steady-state creep only; primary creep is discussed in Chapter 17, Section 17.1.
If
the activation energy ∆F in eqn. (2.9) or ∆Fp in eqn.
(2.12) is small, then thermally-activated glide can lead to creep-like
behavior above 0.3TM.
The activation of dislocation segments over obstacles leads to a drift
velocity which, in the limit of very small ∆F, approaches a linear dependence on
stress. This, coupled with the
stress-dependence of the mobile dislocation density (eqn. (2.3)) leads to a behavior which resembles power-law
creep with 
.
This glide-controlled creep may be important in ice (Chapter 16)
and in certain ceramics (Chapters 9 to 15), and perhaps, too, in metals below
0.5TM.
The maps of later chapters include the predictions of the glide mechanisms discussed in Section 2.2; to that extent, glide-controlled creep is included in our treatment. But our approach is unsatisfactory in that creep normally occurs at or near steady state, not at constant structure—and eqns. (2.9) and (2.12) describe only this second condition. A proper treatment of glide-controlled creep must include a description of the balanced hardening-and-recovery processes which permit a steady state. Such a treatment is not yet available.
At high temperatures, dislocations acquire a new degree of freedom: they can climb as well as glide (Fig. 2.4). If a gliding dislocation is held up by discrete obstacles, a little climb may release it, allowing it to glide to the next set of obstacles where the process is repeated. The glide step is responsible for almost all of the strain, although its average velocity is determined by the climb step. Mechanisms which are based on this climb-plus-glide sequence we refer to as climb-controlled creep (Weertman, 1956, 1960, 1963) [19-21]. The important feature which distinguishes these mechanisms from those of earlier sections is that the rate-controlling process, at an atomic level, is the diffusive motion of single ions or vacancies to or from the climbing dislocation, rather than the activated glide of the dislocation itself.
Fig. 2.4. Power-law creep involving cell-formation by climb. Power-law creep limited by glide processes alone is also possible.
Above 0.6TM climb is generally lattice-diffusion controlled. The velocity υc at which an edge dislocation climbs under a local normal stress an acting parallel to its Burgers' vector is (Hirth and Lothe, 1968) [22]:
|
|
(2.17) |
where Dυ
is the lattice
diffusion coefficient and Ω the atomic or ionic volume. We obtain
the basic climb-controlled creep equation by supposing that
σn is proportional to
the applied stress σs, and that the average velocity of the
dislocation, 
,
is proportional to the rate at which it climbs, υc. Then, combining eqns. (2.2), (2.3)
and (2.17) we obtain:
|
|
(2.18) |
where we have approximated Ω by b3, and incorporated all the constants of proportionality into the dimensionless constant, A1, of order unity.
Some materials obey this equation: they exhibit proper-law creep with a power of 3 and a constant A1 of about 1 (see Brown and Ashby, 1980a [23]). But they are the exceptions rather than the rule. It appears that the local normal stress, σn, is not necessarily proportional to σs implying that dislocations may be moving in a cooperative manner which concentrates stress or that the average dislocation velocity or mobile density varies in a more complicated way than that assumed here. Over a limited range of stress, up to roughly 10-3μ, experiments are well described by a modification of eqn. (2.18) (Mukherjee et al., 1969) [24] with an exponent, n, which varies from 3 to about 10:
|
|
(2.19) |
Present theoretical models for this behavior are unsatisfactory. None can convincingly explain the observed values of n; and the large values of the dimensionless constant A2 (up to 1015) strongly suggest that some important physical quantity is missing from the equation in its present form (Stocker and Ashby,1973; Brown and Ashby,1980) [23, 25]. But it does provide a good description of experimental observations, and in so far as it is a generalization of eqn. (2.18), it has some basis in a physical model.
In this simple form, eqn. (2.19) is incapable of explaining certain experimental facts, notably an increase in the exponent n and a drop in the activation energy for creep at lower temperatures. To do so it is necessary to assume that the transport of matter via dislocation core diffusion contributes significantly to the overall diffusive transport of matter, and—under certain circumstances—becomes the dominant transport mechanism (Robinson and Sherby, 1969) [26]. The contribution of core diffusion is included by defining an effective diffusion coefficient (following Hart, 1957 [27] and Robinson and Sherby, 1969 [26]):
|
|
where Dc is the core diffusion coefficient, and fυ and fc are the fractions of atom sites associated with each type of diffusion. The value off is essentially unity. The value of fc is determined by the dislocation density, ρ:
|
|
where ac is the cross-sectional area of the dislocation core in which fast diffusion is taking place. Measurements of the quantity acDc have been reviewed by Balluffi (1970) [28]: the diffusion enhancement varies with dislocation orientation (being perhaps 10 times larger for edges than for screws), and with the degree of dissociation and therefore the arrangement of the dislocations. Even the activation energy is not constant. But in general, Dc is about equal to Db (the grain boundary diffusion coefficient), if ac is taken to be 2δ2 (where δ is the effective boundary thickness). By using the common experimental observations* that ρ ≈ 10/b2 (σs/μ)2 (eqn. 2.3), the effective diffusion coefficient becomes:
|
|
(2.20) |
When inserted into eqn. (2.19), this gives the rate equation for power-law creep†:
|
|
(2.21) |
Eqn.
(2.21) is really two rate-equations. At high temperatures and low
stresses, lattice diffusion is dominant; we have called the resulting field hightemperature
creep (“H.T. creep”). At lower temperatures, or higher stresses, core
diffusion becomes dominant, and the strain rate varies as
instead of
; this field
appears on the maps as lowtemperature creep (“L.T. creep”).
* The observations of Vandervoort (1970) [32], for example, show that ρ ≈ β/b2 (σs/μ) for tungsten in the creep regime.
† Eqn.
(2.21) is equally written in terms of the tensile stress and strain-rate.
Our constant A2 (which
relates shear stress to shear strain-rate) is related to the equivalent
constant A which appears in tensile forms of this equation by 
.
For further discussion see Chapter 4. The later tabulations of data list
the tensile constant, A.
There
is experimental evidence, at sufficiently low stresses, for a dislocation creep
mechanism for which is proportional
to σs. The effect
was
first noted in aluminium by Harper and Dorn (1957) [29] and Harper et al. (1958)
[30]: they observed linearviscous creep, at stresses below 5 x10-6
μ, but at
rates much higher than those possible by diffusional flow (Section 2.5). Similar
behavior
has been observed in lead and tin by Mohamed et al. (1973) [31]. The
most
plausible explanation is that of climb controlled creep under conditions such
that the dislocation density does not change with stress. Mohamed et al. (1973)
[31] summarize data showing a constant, low dislocation density of about 108 /m2 in the Harper-Dorn
creep range. Given this constant density, we obtain a rate-equation by
combining eqns. (2.2) and (2.17), with
, to give:
|
|
(2.22) |
This is conveniently rewritten as:
|
|
(2.23) |
where AHD = ρmΩb is a dimensionless constant.
Harper-Dorn creep is included in the maps for aluminium and lead of Chapter 4, using the experimental value for AHD of 5 x 10-11 for aluminium (Harper et al., 1958) [30] and of 1.2 x 10-9 for lead (Mohamed et al., 1973) [31]. They are consistent with the simple theory given above if ρ = 108 - 109/m2. The field only appears when the diffusional creep fields are suppressed by a large grain size. Harper-Dorn creep is not shown for other materials because of lack of data.
At high stresses (above about 10-3 μ), the simple power-law breaks down: the measured strain-rates are greater than eqn. (2.21) predicts. The process is evidently a transition from climb-controlled to glide-controlled flow (Fig. 2.5). There have been a number of attempts to describe it in an empirical way (see, for example, Jonas et al., 1969 [33]). Most lead to a rate-equation of the form:
|
|
(2.24) |
or the generalization of it (Sellars and Tegart, 1966 [34]; Wong and Jonas, 1968 [35]):
|
|
(2.25) |
which at low stresses (β'σs < 0.8) reduces to a simple power-law, while at high (β'σs > 1.2) it becomes an exponential (eqn. (2.4)).
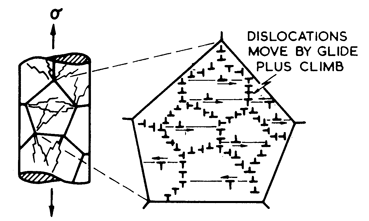
Fig. 2.5. Power-law breakdown: glide contributes increasingly to the overall strain-rate.
Measurements of the activation energy Qcr in the power-law breakdown regime often give values which exceed that of self-diffusion. This is sometimes taken to indicate that the recovery process differs from that of climb-controlled creep. Some of the difference, however, may simply reflect the temperature-dependence of the shear modulus, which has a greater effect when the stress-dependence is greater (in the exponential region). A better fit to experiment is then found with:
|
|
with α'=β'μ0. In order to have an exact correspondence of this equation with the power-law eqn. (2.21) we propose the following rate-equation for power-law creep and power-law breakdown
|
|
(2.26) |
where
and
Eqn. (2.26) reduces identically to the power-law creep equation (2.21) at stresses below σs ≈ μ/α'. There are, however, certain difficulties with this formulation. The problem stems from the use of only two parameters, n' and α', to describe three quantities: n' describes the power-law; α' prescribes the stress level at which the power-law breaks down; and n' α', describes the strength of the exponential stress-dependence. Lacking any physical model, it must be considered fortuitous that any set of n' and α', can correctly describe the behavior over a wide range of stresses.
In spite of these reservations, we have found that eqn. (2.26) gives a good description of hot working (power-law breakdown) data for copper and aluminium. Because we retain our fit to power-law creep, the value of n' is prescribed, and the only new adjustable parameter is α'. This will be discussed further in Chapter 4, and Chapter 17, Section 17.2, where values for α', are given.
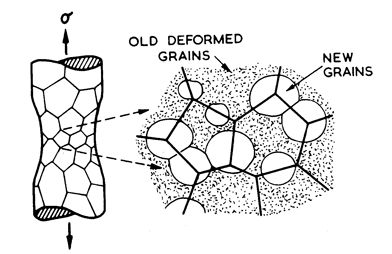
Fig.2.6. Dynamic recrystallization replaces deformed by undeformed material, permitting a new wave of primary creep, thus accelerating the creep rate.
At high temperatures (≥ 0.6 TM) power-law creep may be accompanied by repeated waves recrystallization as shown in Fig. 2.6 (Hardwick et al., 1961 [36]; Nicholls and McCormick, 1970 [37]; Hardwick and Tegart, 1961 [38]; Stūwe, 1965 [39]; Jonas et al., 1969 [33]; Luton and Sellars,1969 [40]). Each wave removes or drastically changes the dislocation substructure, allowing a period of primary creep, so that the strain-rate (at constant load) oscillates by up to a factor of 10. The phenomenon has been extensively studied in Ni, Cu. Pb, Al and their alloys (see the references cited above), usually in torsion but it occurs in any mode of loading. It is known to occur in ceramics such as ice and NaCl, and in both metals and ceramics is most pronounced in very pure samples and least pronounced in heavily alloyed samples containing a dispersion of stable particles.
Dynamic recrystallization confuses the hightemperature, high-stress region of the maps. When it occurs the strain-rate is higher than that predicted by the steady-state eqn. (2.21), and the apparent activation energy and creep exponent may change also (Jonas et al., 1969 [33]). The simplest physical picture is that of repeated waves of primary creep, occurring with a frequency which depends on temperature and strain-rate, each wave following a primary creep law (Chapter 17, Section 17.1) and having the same activation energy and stress dependence as steady-state creep. But a satisfactory model, even at this level, is not yet available.
Accordingly, we adopt an empirical approach. The maps shown in Chapter 1 and in Chapters 4 to 16, show a shaded region at high temperatures, labelled “dynamic recrystallization”. It is not based on a rate-equation (the contours in this region are derived from eqn. (2.21)), but merely shows the field in which dynamic recrystallization has been observed, or in which (by analogy with similar materials) it would be expected.
A solid solution influences creep in many ways. The lattice parameter, stacking fault energy, moduli and melting point all change. Diffusive transport now involves two or more atomic species which may move at different rates. Solute atoms interact with stationary and moving dislocations introducing a friction stress for glide-controlled creep and a solute-drag which retards climb-controlled creep (see Hirth and Lothe, 1968 [22] for details of these interactions). If the alloy is ordered, a single moving dislocation generally disrupts the order; if they move in paired groups, order may be preserved, but this introduces new constraints to deformation (see Stoloff and Davies, 1967 [41]).
The stress dependence of creep in solid solutions falls into two classes (Sherby and Burke, 1967 [42]; Bird et al., 1969 [43]): those with a stress dependence of n = 4 to 7; and those with n ≈ 3. The first class resembles the pure metals, and is referred to as “climbcontrolled creep”. The second is referred to as “viscous-drag-controlled creep” and is believed to result from the limitation on dislocation velocity imposed by the dragging of a solute atmosphere, which moves diffusively to keep up with the dislocation. To a first approximation, both classes of creep behavior may be described by the powerlaw creep equation (eqn. (2.21)), with appropriate values of n, A, and diffusion coefficients. That is what is done here.
The diffusion coefficient for vacancy diffusion, appropriate for climb-controlled creep in a twocomponent system, is:
|
|
(2.27) |
where DA and DB are the tracer diffusion coefficients of components A and B. respectively, and xA and xB are the respective atomic fractions (Herring,1950 [44]; Burton and Bastow, 1973 [45]). The appropriate diffusion coefficient for viscous-drag-controlled creep is the chemical interdiffusivity of the alloy:
|
|
(2.28) |
where γA is the activity coefficient of the A species. (This average applies because the solute atmospherediffuses with the dislocation by exchanging position with solvent atoms in the dislocation path.)
Low-temperature, core-diffusion, limited creep should occur in solid solutions by the same mechanism as in pure metals. The diffusion coefficient must be changed, however, to take into account the solute presence, in the way described by eqn. (2.27). In general, the solute concentration at the dislocation core will differ from that in the matrix, and core diffusion will be accordingly affected; but the lack of data means that diffusion rates have to be estimated (Brown and Ashby, 1980b [46]; see also Chapters 7 and 8). Solid solutions exhibit power-law breakdown behavior at high stresses, and Harper-Dorn creep at low stresses.
A dispersion of strong particles of a second phase blocks dislocation glide and climb, helps to stabilize a dislocation substructure (cells), and may suppress dynamic recrystallization. The stress exponent n is found to be high for dispersion-hardened alloys: typically 7 or more; and the activation energy, too, is often larger than that for self-diffusion. Creep of dispersion-hardened alloys is greatly influenced by thermomechanical history. Cold working introduces dislocation networks which are stabilized by the particles, and which may not recover, or be removed by recrystallization, below 0.8 or 0.9 TM. The creep behavior of the cold-worked material then differs greatly from that of the recrystallized material, and no steady state may be possible. On recrystallization, too, the particles can stabilize an elongated grain structure which is very resistant to creep in the long direction of the grains.
Early theories of creep in these alloys (Ansell, 1968 [47]) were unsatisfactory in not offering a physical explanation for the high values of n and Q.The work of Shewfelt and Brown (1974, 1977) [48, 49] has now established that creep in dispersion-hardened single crystals is controlled by climb over the particles. But a satisfactory model for polycrystals (in which grain boundary sliding concentrates stress in a way which helps dislocations overcome the dispersion) is still lacking.
Most precipitates, when fine, are not stable at creep temperatures, but may contribute to shortterm creep strength: alloys which precipitate continuously during the creep life often have good creep strength. When coarse, a precipitate behaves like a dispersion.
A stress changes the chemical potential, φ, of atoms at the surfaces of grains in a polycrystal. A hydrostatic pressure changes φ everywhere by the same amount so that no potential gradients appear; but a stress field with a deviatoric component changes φ on some grain surfaces more than on others, introducing a potential gradient, ∆φ. At high temperatures this gradient induces a diffusive flux of matter through and around the surfaces of the grains (Fig. 2.7), and this flux leads to strain, provided it is coupled with sliding displacements in the plane of the boundaries themselves. Most models of the process (Nabarro, 1948; Herring, 1950; Coble, 1963; Lifshiftz, 1963; Gibbs. 1965; Rag and Ashby, 1971) assume that it is diffusion-controlled. They are in substantial agreement in predicting a rate-equation: if both lattice and grain boundary diffusion are permitted, the rate-equation for diffusional flow is:
|
|
(2.29) |
| where |
|
(2.30) |
Here d is the grain size, Db is the boundary diffusion coefficient and δ the effective thickness of the boundary.
Like the equation for climbed-controlled creep, it is really two equations. At high temperatures, lattice diffusion controls the rate; the resulting flow is known as Nabarro-Herring creep and its rate scales as Dυ/d2. At lower temperatures, grain-boundary diffusion takes over; the flow is then called Coble creep, and scales as Db/d3.
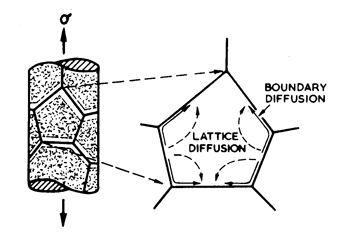
Fig 2.7. Diffusional flow by diffusional transport through and round the grains. The strain-rate may be limited by the rate of diffusion or by that of an interface reaction.
This equation is an oversimplification; it neglects the kinetics involved in detaching vacancies from grain-boundary sites and reattaching them again, which may be important under certain conditions. Such behavior can become important in alloys, particularly those containing a finely dispersed second phase. Pure metals are well described by eqn. (2.29), and it is used, in this form, to construct most of the maps of subsequent sections. Interface reaction control, and its influence on the maps, is dealt with further in Chapter 17, Section 17.3.
A solid
solution may influence diffusional flow by changing the diffusion
coefficient (Herring, 1950 [44]). When lattice diffusion is dominant, the coefficient
Dυ should be replaced
by 
(eqn.
(2.27)). When boundary diffusion is dominant a similar combined coefficient
should be used, but lack of data makes this refinement impossible at present.
More important, the solid solution can impose a drag on boundary dislocations
slowing the rate of creep; and solute redistribution during diffusional flow
can lead to long transients. These effects are discussed further in Chapter 17,
Section 17.3.
There is evidence that a dispersion of a second phase influences the way in which a grain boundary acts as a sink and source of vacancies, introducing a large interface-reaction barrier to diffusion and a threshold stress below which creep stops. Its influence is illustrated in Chapter 7, and discussed in Chapter 17, Section 17.3.
The influence of a precipitate on diffusional flow is not documented. This sort of creep is normally observed at high temperatures (> 0.5 TM) when most precipitates will dissolve or coarsen rapidly.
1. Tyson, W.R., Theoretical Strength of Perfect Crystals. Phil. Mag, 1966. 14: p. 925-936.
2. Kelly, A., Strong Solids. 1966: Oxford University Press.
3. MacKenzie, J.K. 1959, Bristol University.
4. Orowan, E. Problems of plastic gliding. in Proc. Phys. Soc. 1940.
5. Argon, A.S., Internal stresses arising from the interaction of mobile dislocation. Scripta Metallurgica (before 1990), 1970. 4: p. 1001.
6. Evans, A.G. and R.D. Rawlings, Thermally activated deformation of crystalline materials. Phys. Stat. Sol., 1969. 34: p. 9-31.
7. Kocks, U.F., A.S. Argon, and M.F. Ashby, Prog. Mat. Sci., 1975. 19: p. 1.
8. de Meester, B., et al., Thermally activated deformation in crystalline solids, in Rate Processes in Plastic Deformation, J.C.M.L.a.A.K. Mukherjee, Editor. 1973, A.S.M. p. 175-226.
9. Guyot, P. and J.E. Dorn, A Critical Review of the Peierls Mechanism. Can. J. Phys., 1967. 45: p. 983-1016.
10. Raffo, P.L., Yielding and fracture in tungsten and tungsten-rhenium alloys. J. Less Common Metals, 1969. 17: p. 133-49.
11. Ashby, M.F., A first report on deformation-mechanism maps. Acta Metallurgica (pre 1990), 1972. 20: p. 887.
12. Kocks, U.F., The relation between polycrystal deformation and single-crystal deformation. Met. Trans., 1970. 1: p. 1121.
13. Klahn, D., A.K. Mukherjee, and J.E. Dorn. in Second International Conference on the Strength of Metals and Alloys. 1970. Asilomar, California: ASM.
14. Kumar, A., F.E. Hauser, and J.E. Dorn, Viscous drag on dislocations in aluminum at high strain rates. Acta Metallurgica (pre 1990), 1968. 16: p. 1189.
15. Kumar, A. and R.C. Kumble, Viscous drag on dislocations at high strain rates in copper. Journal of Applied Physics, 1969. 40: p. 3475-80.
16. Brown, L.M. and W.M. Stobbs, The Work-hardening of Copper-Silica: I. A Model Based on Internal Stresses, with no Plastic relaxation. Philosophical Magazine( before 1978), 1971. 23: p. 1185.
17. Hirsch, P.B. and F. Humphries. in Proc. R. Soc. 1970.
18. Bolling, G.F. and R.H. Richman, Continual mechanical twinning. Acta Metallurgica (pre 1990), 1965. 13: p. 709, 723.
19. Weertman, J., Creep of polycrystalline aluminium as determined from strain rate tests. J. Mech. Phys. Solids, 1956. 4: p. 230-234.
20. Weertman, J., Creep of indium, lead and some of their alloys with various other metals. Trans. AIME, 1960. 218: p. 207-18.
21. Weertman, J., Discussion of: " An Experimental relation defining the stress dependence of minimun creep rate in metals". Trans. AIME, 1963. 227: p. 1475-76.
22. Hirth, J.P. and J. Lothe, Theory of Dislocations. 1968: McGraw-Hill. 435.
23. Brown, A.M. and M.F. Ashby, Correlations for diffusion constants. Acta Metallurgica (pre 1990), 1980a. 28: p. 1085.
24. Mukherjee, A.K., J.E. Bird, and J.E. Dorn, Experimental correlation for high-temperature creep. Trans. ASM, 1969. 62: p. 155-179.
25. Stocker, R.L. and M.F. Ashby, On the empirical constants in the Dorn equation. Scripta Met., 1973. 7: p. 115-20.
26. Robinson, S.L. and O.D. Sherby, Mechanical behaviour of polycrystalline tungsten at elevated temperature. Acta Met., 1969. 17: p. 109.
27. Hart, E.W., On the role of dislocations in bulk diffusion. Acta Metallurgica (pre 1990), 1957. 5: p. 597.
28. Balluffi, R.W., On Measurement of Self-Diffusion rates along Dislocations in F.C.C. Metals. Phys. Stat. Sol., 1970. 42: p. 11-34.
29. Harper, J.G. and J.E. Dorn, Viscous creep of aluminum near its melting temperature. Acta Metallurgica (pre 1990), 1957. 5: p. 654.
30. Harper, J.G., L.A. Shepard, and J.E. Dorn, Creep of aluminum under extremely small stresses. Acta Metallurgica (pre 1990), 1958. 6: p. 509.
31. Mohamed, F.A., K.L. Murty, and J.W. Morris, Jr. in The John E. Dorn Memorial Symposium. 1973. Cleveland, Ohio: ASM.
32. Vandervoort, R.R., The creep behavior of W-5 Re. Met. Trans., 1970. 1: p. 857.
33. Jonas, J.J., C.M. Sellers, and W.J.M. Tegart, Met. Rev., 1969. 14: p. 1-24.
34. Sellars, C.M. and W.J.M. Tegart, La relation entre la resistance et la structure dans la deformation a chaud. Mem. Sci. Rev. Met., 1966. 63: p. 731-46.
35. Wongi, W.A. and J.J. Jonas, Aluminium extrusion as a thermally activated process. Trans. AIME, 1968. 242: p. 2271-2280.
36. Hardwick, D., C.M. Sellars, and W.J.M. Tegart, The Occurence of Recrystallization During High-Temerature Creep. J. Inst. Met., 1961-62. 90: p. 21-23.
37. Nicholls, J.H. and P.G. McCormick, Dynamic recrystallization in lead. Met. Trans., 1970. 1: p. 3469.
38. Hardwick, D. and W.J. McG Tegart, Structural changes during the deformation of copper, aluminium and nickel at high temperatures and strain rate. J. Inst. Met., 1961-62. 90: p. 17-21.
39. Stuwe, H.P., Dynamische erholung bei der warmverformung. Acta Met., 1965. 13: p. 1337.
40. Luton, M.J. and C.M. Sellars, Dynamic recrystallization in nickel and nickel-iron alloys during high temperature deformation. Acta Metallurgica (pre 1990), 1969. 17: p. 1033.
41. Stoloff, N.S. and R.G. Davies, Prog. Mat. Sci., 1967. 13: p. 1.
42. Sherby, O.D. and P.M. Burke, Mechanical behavior of crystalline solids at elevated temperature. Prog. Mat. Sci., 1967. 13: p. 325.
43. Bird, J.E., A.K. Mukherjee, and J.F. Dorn, Correlations Between High-Temperature Creep Behaviour and Structure, D.G.a.R. Brandon, A., Editor. 1969, Haifa University Press, Israel. p. 255-341.
44. Herring, C., Diffusional viscosity of a polycrystalline solid. Journal of Applied Physics, 1950. 21: p. 437.
45. Burton, B. and B.D. Bastow, The diffusional creep of binary copper alloys. Acta Metallurgica (pre 1990), 1973. 21: p. 13.
46. Brown, A.M. and M.F. Ashby, On the power-law creep equation. Scripta Metallurgica (before 1990), 1980b. 14: p. 1297.
47. Ansell, G.S., The mechanism of dispersion strenghtening, in Oxide Dispersion Strengthening. 1968, AIME, Gordon & Breach. p. 61-141.
48. Shewfelt, R.S.W. and L.M. Brown, High-temperature strength of dispersion-hardened single cryssitals- I. Experiemntal results. Phil Mag., 1974. 30: p. 1135-45.
49. Shewfelt, R.S.W. and L.M. Brown, High-temperature strength of dislocation-hardened single crystals-II. Theory. Phil. Mag., 1977. 35: p. 945-62.